目次

０　はじめに

１　具体例１　合不合判定テスト

２　具体例１－１　正答率約50％の問題

３　具体例１－２　正答率約25％の問題

４　具体例２　海城中学校の入試問題

５　まとめ

はじめに

いきなりですが、質問です。

中学入試で偏差値60台の学校の合否を分ける問題がどれくらいの難易度かおわかりになりますか？

即答できる保護者は少ないと思います。

塾講師でも即答できる人は多くありませんから。

偏差値60以上は成績上位15％にあたります。

では、成績上位15％に入るためには上位15％しか解けない問題を解けなくてはならないのでしょうか？

答えはノーです。

成績上位15％に入るためには２人に１人が解ける問題を解ければよいということを以下でエビデンスをあげながら明らかにします。

１　具体例１　合不合判定テスト

それでは、早速、問題を具体的に見ていきましょう。

まずは、2023年12月に実施された最終回の四谷大塚の合不合判定テストの算数の問題を取りあげます。

合不合判定テストとは、１万人以上の受験者が受ける、もっとも代表的な志望校判定テストのことです。

しかも、上位層から下位層まで幅広く受験者を集めているのが合不合判定テストの特徴です。

入試問題ではありませんが、各問題に対する正答率がわかりますので、中学入試で合否を分ける問題がどれほどの難易度かということを入試問題以上にわかりやすく示すことができます。

入試問題は後ほど取りあげます。

２　具体例１－１　正答率約50％の問題

さて、四谷大塚の資料によれば、男子で正答率50％以上の問題をすべて解けば、偏差値は54です。

四谷大塚の偏差値は合格可能性80％の偏差値ですので、偏差値54だと、偏差値55までの学校はおさえ校、偏差値50台後半の学校は受かる可能性もあれば落ちる可能性もある学校となります。

では、正答率約50％の問題を具体的に見てみましょう。

まずは合不合判定テストの問題です。

秒速20ｍで走る貨物列車と、秒速25ｍで走る急行列車があります。ある鉄橋をわたり始めてからわたり終わるまでに貨物列車は23秒、急行列車は16秒かかります。また、貨物列車と急行列車がすれちがうのにかかる時間は12秒です。急行列車の長さは何ｍですか。（答え　240m）

この問題は四谷大塚の５年夏期講習の教科書の必修編第５回の例題１と例題２を合わせた問題と言えます。

教科書の問題は次のものです。

例題１(2)　長さ200mの電車が秒速20mで走っています。この電車が、長さ500mのトンネルにさしかかってから完全にトンネルをぬけるまでに何秒かかりますか。（答え　35秒）

例題２(1)　長さ160mで秒速25mで走る電車Ａと、長さ240mで秒速15mで走る電車Ｂがあります。ＡとＢが向かい合って走っているとき、２つの電車がすれちがい始めてからすれちがい終わるまでに何秒かかりますか。（答え　10秒）

合不合判定テストの問題は複合問題ですが、２つの例題を単純に足し合わせただけの問題ですので、標準的な難易度だと言っていいでしょう。

実際に、受験者の２人に１人が正解しています。

これが偏差値50台後半の学校で合否を分ける問題となります。

３　具体例１－２　正答率約25％の問題

次の例にいきましょう。

やはり四谷大塚の資料によれば、男子で正答率が約25％以上の問題をすべて解けば、偏差値は60を越え、偏差値60以下の学校はおさえ校、偏差値60台前半の学校は受かる可能性も落ちる可能性もある学校となります。

まずは、合不合判定テストで正答率約25％の問題です。

２けたの整数Ａ、Ｂ(Ａ＜Ｂ)の最大公約数が２、最小公倍数が2024です。Ａ、Ｂをそれぞれ求めなさい。（答え　Ａ＝46、Ｂ＝88）

これは四谷大塚の教科書の予習シリーズ・５年下・第13回例題５の類題です。

予習シリーズの例題は以下のものです。

２つの整数Ａ、Ｂがあります。ＢはＡより大きく、ＡとＢの最大公約数は６、最小公倍数は144です。Ａ、Ｂの組として考えられるものを（Ａ、Ｂ）の形ですべて答えなさい。（答え　（６、144）、（18、48））

合不合判定テストの問題は、５年生の教科書の例題の類題ですから、標準的な難易度だと言えましょう。

しかし、途中の計算がやや大変なので、4人に１人しか正解できていません。

これが偏差値60台前半で合否を分ける問題となります。

４　具体例２　海城中学校の入試問題

最後に、入試問題を見ておきましょう。

海城中学校の2023年第１回の問題を取りあげます。

海城中学校は、男子御三家、共学トップの渋渋、付属トップの早慶に次いで入るのが難しい男子校です。

一般に入試問題の難易度は偏差値に対応していますので、海城中学校より難しい問題を出すのは海城中学校より偏差値の高い数校くらいしかありません。

この年の海城の問題は、前半の1～３番が塾の教科書の例題としてよく目にするような問題で、後半の４～６番が少し見慣れない問題です。

中学校が発表しているデータから推測すると、前半の１～３番を確実に解き切って、後半の問題で小問を拾えば、合格ラインに達します。

後半の問題の中には点数の取りやすい小問が含まれていますので、前半の１～３番を確実に解き切れるかどうかが勝負を分けます。

ここでは前半で一番難しい問題を取りあげます。

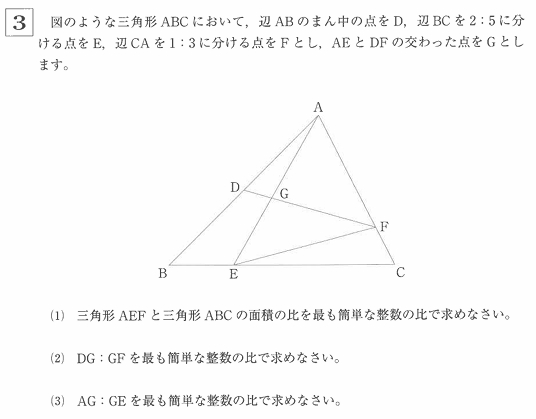
（答え　(1)　15：28　(2)　４：15　(3)　21：17　)

これが四谷大塚の教科書の予習シリーズ・５年下・第８回例題４の類題であることは簡単に見抜けるでしょう。

（答え　10：３）

いずれの問題も標準やや難くらいの難易度でしょう。

正答できるのは全体の４人に１人といったところでしょうか。

切りがありませんので、例をあげるのは以上にします。

なお、ここでは男子だけを見ましたが、女子や共学はもっと難易度が低くなります。

５　まとめ

まとめましょう。

以上で見てきたように、最上位の数校を除けば、塾のテキストで何度も解いた標準的な難易度の問題を確実に解くことができれば、合格できます。

しかも、経験上、テストは時間が限られていますが、時間をもう少し多く与えれば、正答率50％の問題は正答率80％くらいに、正答率25％の問題は正答率50％くらいに上がります。

例えば、偏差値60以上の成績上位15％に入るためには、全体の正答率が50％の問題が解ければよいということになります。

受験生の大半にとって、合否を分ける問題は難しいものではなく、時間があれば、解けるはずの問題なのです。