目次
0 はじめに
1 理系の大学教育について
2 秘伝のワザ その1 ざっくり計算
3 秘伝のワザ その2 数の大きさの吟味
4 秘伝のワザ その3 計算結果が正しいと仮定しての吟味
5 まとめ
はじめに
今回は、中学受験でもっとも点差のつきやすい算数のミス対策について説明させていただきます。
私は理系出身ですが、私の知る限り、文系出身のセンセイが教えるミス対策はほとんど効果がありません。
書籍や動画の中に登場するのはどうしても文系出身のセンセイが多いのですが、文系出身のセンセイの言うことは、ミス対策に関しては、あまり信用しない方がよいでしょう。
文系出身のセンセイの言っていることは、煎じ詰めれば、意識改革にすぎません。
意識改革も必要ですが、意識改革は難しいのです。
意識改革がそんなに簡単にできないからこそ、保護者の悩みは尽きないわけです。
でも、ご安心下さい。
そもそも意識改革はミス対策としてはあまり効果がありませんので、意識改革は不要です。
では、ミスを減らすために必要なのは何でしょうか?
ミスを減らすために必要なのは、ミスを減らすための具体的な技術です。
1 理系の大学教育について
私が理系の大学教育の中で徹底的に叩き込まれたのは、計算結果がつじつまが合っているのかどうかを確かめる技術でした。
例えば、ゼミ発表でも、先生がツッコむのは、計算結果がつじつまが合っているのかどうかということばかりでした。
テーマなどは二の次でした。
徹底的に教え込まれたのは、計算結果を確かめるために、次元やオーダーを確かめる技術や、計算結果が正しいと仮定して、そのもっともらしさを吟味する技術でした。
ちなみに、ここで言う次元とは、とりあえず単位のことだと思って下さい。
また、オーダーとは、桁数の違いによる数の大きさの違いのことです。
例えば、50万円に比べれば、桁数の小さい5万円と6万円の差は小さく感じますよね。
簡単に言えば、これがオーダーの違いです。
なお、就活で必須の知識となっていると話題のフェルミ推定は、簡単に言えば、オーダーの推定のことです。
こうした理系の大学教育の秘伝の技術を応用したのが私のミス対策の指導法です。
以下では、その指導法のポイントを具体例を使って説明します。
2 秘伝のワザ その1 ざっくり計算
まずは、<秘伝のワザ その1 ざっくり計算>。
たまたま手もとにあった計算問題集をパラパラめくって、テキトーに取り出したのが次の計算問題です。
中学入試で頻出の標準的な計算問題です。
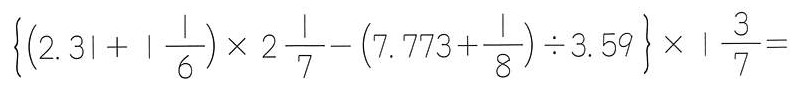
かりに計算結果が13となったとします。
その場合、とりあえずはざっくりと、
{(2.3+1.2)×2-(7.8+0.2)÷4}×1.5=7.5
のように計算してみるのです。
先ほどの13という計算結果が計算ミスであることがわかります。
なお、たまたまですが、ざっくり計算の通り、正解は7.5です。
ざっくり計算は、訓練次第では、正確な計算にかなり近いものとなります。
ただ、そこまでいかなくても、多少の訓練でミスを防ぐことには役立ちます。
3 秘伝のワザ その2 数の大きさの吟味
続いて、<秘伝のワザ その2 数の大きさの吟味>。
答えの数の大きさがもっともらしいかどうかを吟味することで、小学生の場合、かなり多くのミスが防げます。
つい最近も、太郎君の走る速さを秒速100mと答えている生徒がいました。
太郎君、すごすぎだろ…
自動車の速さが時速4000kmという答えもありました。
夢のスーパーカー爆誕!?
食塩水の濃度を50%と答えている生徒もいました。
そんな濃い食塩水作れないから…
4 秘伝のワザ その3 計算結果が正しいと仮定しての吟味
次に、<秘伝のワザ その3 計算結果が正しいと仮定しての吟味>。
これまた計算問題集をパラパラめくって、テキトーに取り出した計算問題です。
やはり中学入試で頻出の標準的な計算問題です。
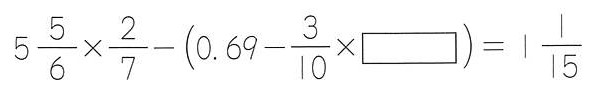
これを平気で4とか答える生徒がいますが、ありえません。
4が正しいとすると、( )の中が(0.69-1.2)となり、マイナスになってしまいます。
中学受験ではマイナスは出てきませんので、計算ミスだとわかります。
逆算は、計算結果を左辺の▢にあてはめて再計算してみて、右辺の答えになるかどうかを確かめるべきです。
なお、正解は10分の3です。
私のファースト・インプレッションも10分の3でした。
0.69の9を消すために、(0.69ー0.9)にしたいでしょうから。
文章題でも、計算結果が正しいと仮定して、そのもっともらしさを吟味してみるべきです。
次は受験生が苦手とするニュートン算の問題です。
やはり問題集からテキトーに選びました。
あるコンサートホールで開門前に300人が並んでいて、開門後も毎分15人ずつ増えていきます。入場口が1つでは30分で行列がなくなるとき、入場口を3つにすると行列は何分でなくなりますか。
という問題で、例えば10分という答えが出たとします。
そしたら、これが正解だとして、吟味してみるのです。
入場口が1つの場合、300人並んでいて、毎分15人ずつ増えるのですから、30分で
300+15×30=750人
が来ることになります。
ということは、1分間で
750÷30=25人
が入場することになります。
一方、入場口が3つの場合、10分という答えが出たので、
300+15×10=450人
が来ることになります。
ということは、1分間で
450÷10=45人
が入場することになります。
ただし、この場合、入場口は3つですから、1つの入場口から1分間で
45÷3=15人
が入場することになります。
ですが、これでは先ほどの計算結果と矛盾します。
よって、計算ミスをしたということになります。
カンのいい子なら、5分で試してみるでしょう。
5分で
300+15×5=375人
が来ますから、1分間で
375÷5=75人
が入場することになります。
ということは、入場口が3つですので、1つの入場口から1分間で
75÷3=25人
が入場しますが、これで先ほどの計算結果と合います。
切りがないので、例は以上にしておきます。
なお、見直しのために、もう一度最初から計算しなさい、ということがよく言われますが、頭の中を完全に白紙に戻すのは難しいので、同じミスを繰り返すことも多いのです。
もう一度最初から計算するとしても、計算結果がつじつまが合っているかどうかを確かめてからの方がよいでしょう。
そうすると、多くの場合、再計算が不要となり、見直しの時間の短縮にもなります。
5 まとめ
以上、中学入試でもっとも点差のつきやすい算数のミス対策を見てきました。
ざっくり計算、数の大きさの吟味、計算結果が正しいと仮定しての吟味の3つのワザを紹介しました。
他の教科のミス対策は、ミスが致命傷となる可能性が低いので、公開するのは別の機会にさせて下さい。
他の教科でも必要なのは意識改革だけではなく、ミスを防ぐための技術も教えることです。
なお、以上のようなミスを防ぐ技術を教えるのは6年生になってからでよいでしょう。
経験上、6年生以下には難しいからです。
