0 はじめに
1 第5位 「百ます計算」
2 第3・4位 『小学生がたった1日で19×19までかんぺきに暗算できる本』・『ドリル版・インド式かんたん計算法』
3 第2位 『計算名人免許皆伝』
4 第1位 『誰でも身につく!暗算力』
はじめに
いきなりですが、経験上、暗算・漢字ができれば、中学受験になります。
暗算・漢字ができるというのは、暗算・漢字ができるというだけのことではないからです。
頭の中で数を操作して、暗算ができるというのは、算数が得意になる前提条件です。
また、漢字が書けるというのは、社会ができるようになる前提条件です。
よって、今回は中学受験向けの暗算教材を5つ、ランキング形式で紹介させていただきます。
どれも取り組んで損にはならない教材ばかりですので、ぜひ最後までお読み下さい。
第5位 「百ます計算」
たし算・ひき算・かけ算・わり算の練習をするための低学年向けの教材です。
有名な教材ですが、念のため、使用法などを説明させていただきます。
1 このような百ます計算のワクを用意して下さい。
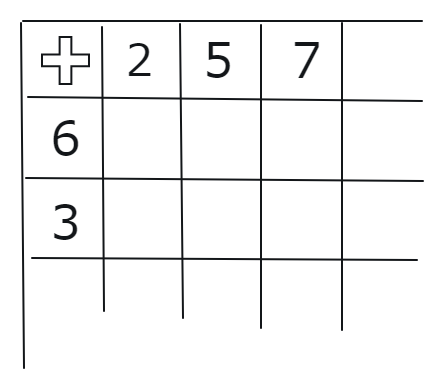
書店で購入できますが、ネットでも無料で手に入れることができます。
2 一番左上に+とあればたし算、-とあればひき算、×とあればかけ算、÷とあればわり算をさせて、ワクをすべてうめさせて下さい。
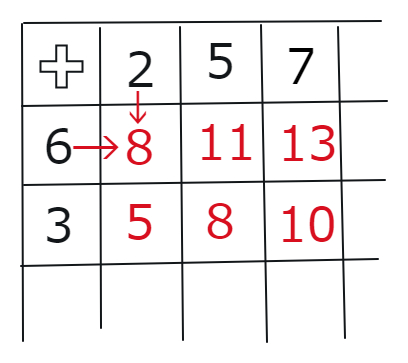
3 キッチンタイマーでタイムを計り、記録して下さい。目安は3~4年生で2分以内とされていますが、他人との比較を目的とするのではなく、自己記録の更新を目標として下さい。
4 毎日、少しずつでかまいませんので、継続すれば、必ず計算力がつきます。
第3・4位 『小学生がたった1日で19×19までかんぺきに暗算できる本』・『ドリル版・インド式かんたん計算法』
どちらも11×11から19×19までの2ケタ×2ケタのインド式暗算法のドリルです。
ベストセラーになっています。
ドリル形式になっていて、子どもだけでも取り組めます。
3~4年生向けの教材でしょう。
念のため、インド式暗算法がどういうものかを説明させていただきます。
たとえば、16×12であれば、
1 12の1の位の2を16にわたして、18×10=180とします。
2 1の位を6×2=12と計算します。
3 最後に、計算結果を合体させ、180+12=192と答えを出します。
中学受験をする場合は、この手順を覚えるだけでなく、次のことをイメージさせながら、計算に取り組ませた方がよいでしょう。
16×12の計算をすることはタテ16・ヨコ12の長方形の面積を求めることと同じです。
1 長方形をタテに切り、タテ16・ヨコ10とタテ16・ヨコ2の2つの長方形に分けます。
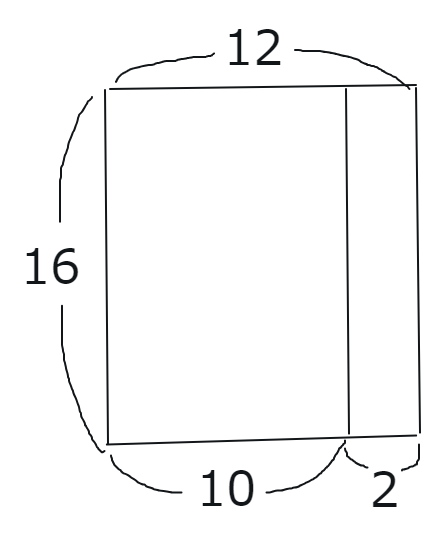
2 2つの長方形を次のように合体させると、タテ18・ヨコ10とタテ2・ヨコ6の2つの長方形ができます。
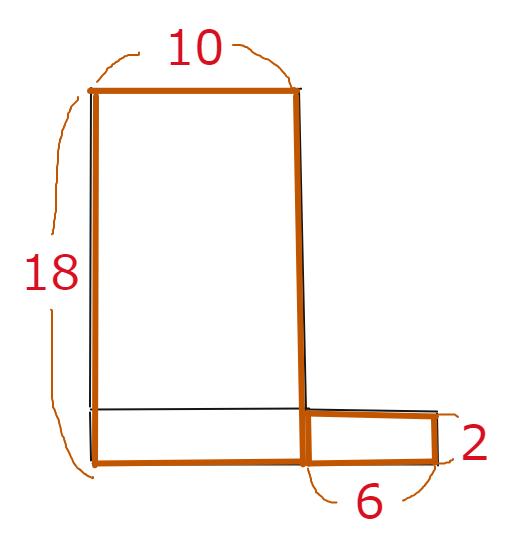
3 ということは、形を変えても、長方形の面積は同じですから、16×12は18×10と6×2を足したものということになります。
算数では、数を何らかの形でイメージすることが大事ですので、ただ計算の手順を覚えるだけでなく、頭の中に長方形を思い浮かべながら計算することを強くオススメします。
第2位 『計算名人免許皆伝』
4年生後半~5年生前半向けの教材でしょう。
塾のテキストに出てくるような計算の仕方がまとめられています。
計算が不得意な場合は取り組んだ方がよいでしょう。
4年生までは計算がしっかりできていれば算数は何とかなるというのが実感です。
また、この教材で一番参考になるのは、計算の際のメモのとり方です。
中学受験の場合は、小学校と違い、問題にメモ書きしながら、計算します。
必須のテクニックですので、ぜひ身につけて下さい。
なお、計算カードが付属していますが、数が少なく、本文は解説中心ですので、子どもの自習向けの教材ではありません。
塾のテキストに取り組むのに苦労している場合、親がこれを読んで教えてあげるという使い方となるでしょう。
第1位 『誰でも身につく!暗算力』
これも4年生後半~5年生前半向けの教材でしょう。
中学校レベルの文字式の計算も含みますが、無視して下さい。
また、これも子どもの自習向けの教材ではありません。
親が解説を参考にお手本を示した上で、子どもに問題を解かせて下さい。
問題数はそれなりにあります。
書籍の中に問題がありますし、QRコードを使って補充問題を手に入れることもできます。
暗算が得意な人が自然に身につけている暗算法を紹介しています。
あげられている暗算法をパーフェクトに身につけさせるというより、暗算のコツを学ぶことができればよいというくらいの感覚で使うとよいでしょう。
暗算の仕方は1つではありません。
各人がやりやすいように暗算すればよいのです。
暗算のコツを身につけることができれば、頭の中で数をイメージして操作することができるようになります。
頭の中で数をイメージして操作できるというのは、算数が得意になる前提条件です。
